Lecture 9.5: Increasing Arity Tail Calls

These notes explore an alternative calling convention that can be used for internal function calls to perform tail call elimination when calling functions of arbitrary arity. These notes are based off of Northeastern University’s CS4410 course. In Lecture 6, we learned how to make C function calls; in Lecture 7, we defined our own functions; in Lecture 9, we started to discuss tail call elimination.

When making calls to C functions, we have no choice but to comply with architecture-specific calling conventions. However, for internal function calls, we can use different (ideally simpler) calling conventions to make compilation easier. Many of the lecture notes discuss a simple, stack-based approach to passing arguments (instead of having to load the first six arguments into registers, as we do when we call into C). We will begin by reviewing this stack-based approach, then introduce our own stack-based approach after exploring design trade-offs.

Review

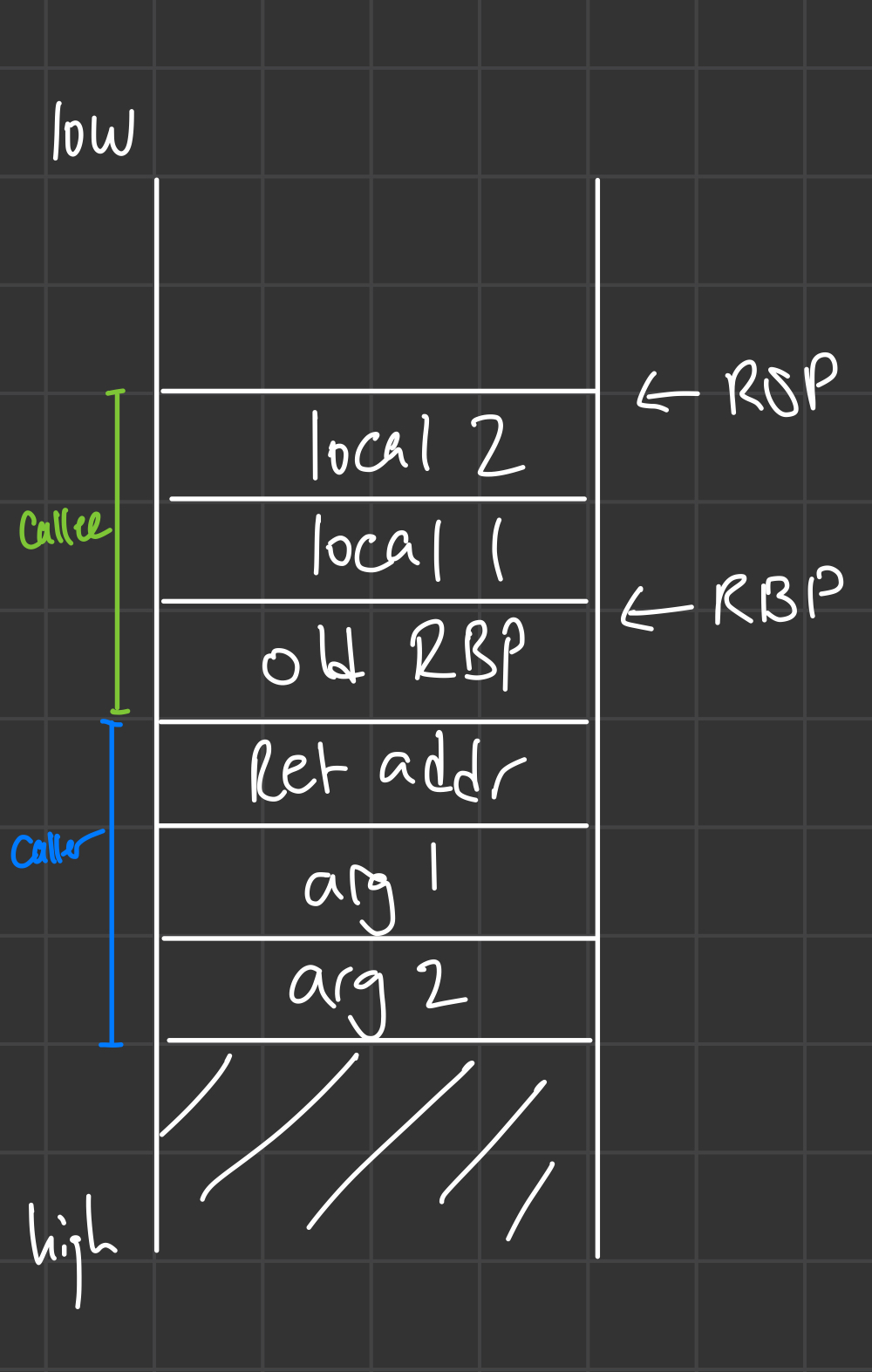
To call a function currently, the caller pushes its arguments onto the stack in reverse order:

push arg_M        ; push last arg first ...
...
push arg_2        ; then the second ...
push arg_1        ; finally the first
call target       ; make the call (which puts return addr on stack)
add RSP, 8*M      ; now we are back: "clear" args by adding 8*numArgs

Note that upon entry to a function, RSP must be a multiple of 16, meaning we actually may need to push an extra padding word onto the stack before arg_M. After the target function returns, we have to increment RSP to clear off the space that the $M$ arguments took up on the stack.

When a function is called, the first thing it must do is store the old RBP onto the stack, since it is a callee-saved register, and decrement RSP to reserve space for its local arguments. Again, we must be careful to keep RSP at a multiple of 16, meaning we may need to reserve an extra padding word here.

push RBP          ; save (previous, caller's) RBP on stack
mov RBP, RSP      ; make current RSP the new RBP
sub RSP, 8*N      ; "allocate space" for N local variables

When a function call is done, we reset RSP and RBP (since they are callee-saved) and return.

mov RSP, RBP      ; restore value of RSP to that just before call
                  ; now, value at [RSP] is caller's (saved) RBP
pop RBP           ; so: restore caller's RBP from stack [RSP]
ret               ; return to caller

In the called function, the first argument can be found at $[RBP + 16]$, and subsequent arguments can be found at $[RBP + 8*(i+1)]$. The first local will still be found at $[RBP - 8]$, and subsequent locals at $[RBP - 8*i]$.

When we compile function declarations, we probably want to structure this somewhat differently:

foo:
foo_prologue:
  push RBP
  mov RBP, RSP
foo_body:
  sub RSP, 8*N
  ; body goes here...
  
  ; to return:
  mov RSP, RBP
  pop RBP
  ret

  ; to make a tail call:
  mov RSP, RBP
  jmp bar_body

Notice how we reserve space for foo’s local variables within foo_body and not foo_prologue. This allows us to make tail calls to functions that use more local arguments, being sure to first reset RSP back to RBP before jumping to that function’s body.

Increasing Arity: What goes wrong?

Many of the problems involving tail calls are discussed in Lecture 9. Many of the problems discussed in the lecture notes come with possible solutions; we will revisit these problems and solutions after introducing our new calling convention. We will reiterate the problem with increasing arity tail calls:

• When we make a tail call, we want to write over the old arguments with our new arguments, then jump to the start of the called function. However, if the called function uses more arguments than we have space for, we have a serious problem. We cannot slot the additional arguments in below the last previous argument, since that would eat into the previous stack frame.

Instead, we could try to shift everything in our current stack frame up, to make space for the new arguments. However, this runs into another problem:

• Suppose we have some function foo that normally calls bar with 2 arguments, which calls baz in tail position with 3 arguments. Clearly, bar will have to shift the stack frame up by one slot to fit the third argument to baz. However, foo will only increment RSP by 16, since it only pushed on two arguments (and had no knowledge that bar will call baz). Now, our stack is misaligned and information is leaking.

Approach 1: Add padding arguments

One natural approach to solving this problem is to analyze which functions are being called from the bodies of other functions. We can track the greatest arity $G$ of a function that could ever possibly be tail called from some function body, then compile that function as if it had $G$ arguments. We will no longer have to shift the stack around to make a tail call, since we reserved space for all $G$ of the arguments we could ever possibly need! In essence, we are turning increasing arity calls into calls with the same or decreasing arity, then using the techniques from before to compile.

Ignoring the work necessary to determine which functions get called by other functions (which could be solved by updating a map of function names to arities until a fixpoint is found, or by constructing a graph of function calls and traversing this graph), there are notable drawbacks here. Of course, lots of space on the stack is being reserved unnecessarily, especially if we were to have a function that makes a tail call to another function with a lot of arguments, but does so infrequently. Not only would the first function have to reserve space for all of those arguments, but anything that calls that function would have to as well.

This approach can work for first-class functions. However, the true problem arises once we have anonymous, higher-order functions. In essence, once we are able to treat functions as values, determining which functions call other functions statically becomes very difficult, if not impossible. Consider a function oh_god_why that constructs a list of functions by calling helper functions which return lists of lambdas, appending them all. Any of these functions can be called by oh_god_why, and we do not know the arities of these functions statically.

Once functions start becoming objects we can manipulate at runtime, as opposed to ones that exist only within our compiler, determining which functions are called gets very undecidable, very quickly. It could be possible to achieve some arity approximation using techniques from dataflow analysis, but this seems quite difficult. For those interested, these notes on static program analysis may be of interest (specifically Chapter 5: Dataflow Analysis with Monotone Frameworks).

Approach 2: Change the convention

As noted above, the problem with shifting our stack frames arises when we have to increment RSP from the caller, since we do not know how many arguments we truly should knock off of the stack. What if we could design an alternative calling convention to prevent the caller from directly incrementing RSP after calling altogether?

Specifically, instead of placing our arguments below RBP and our local variables above it, we can store both our arguments and our local variables above RBP:

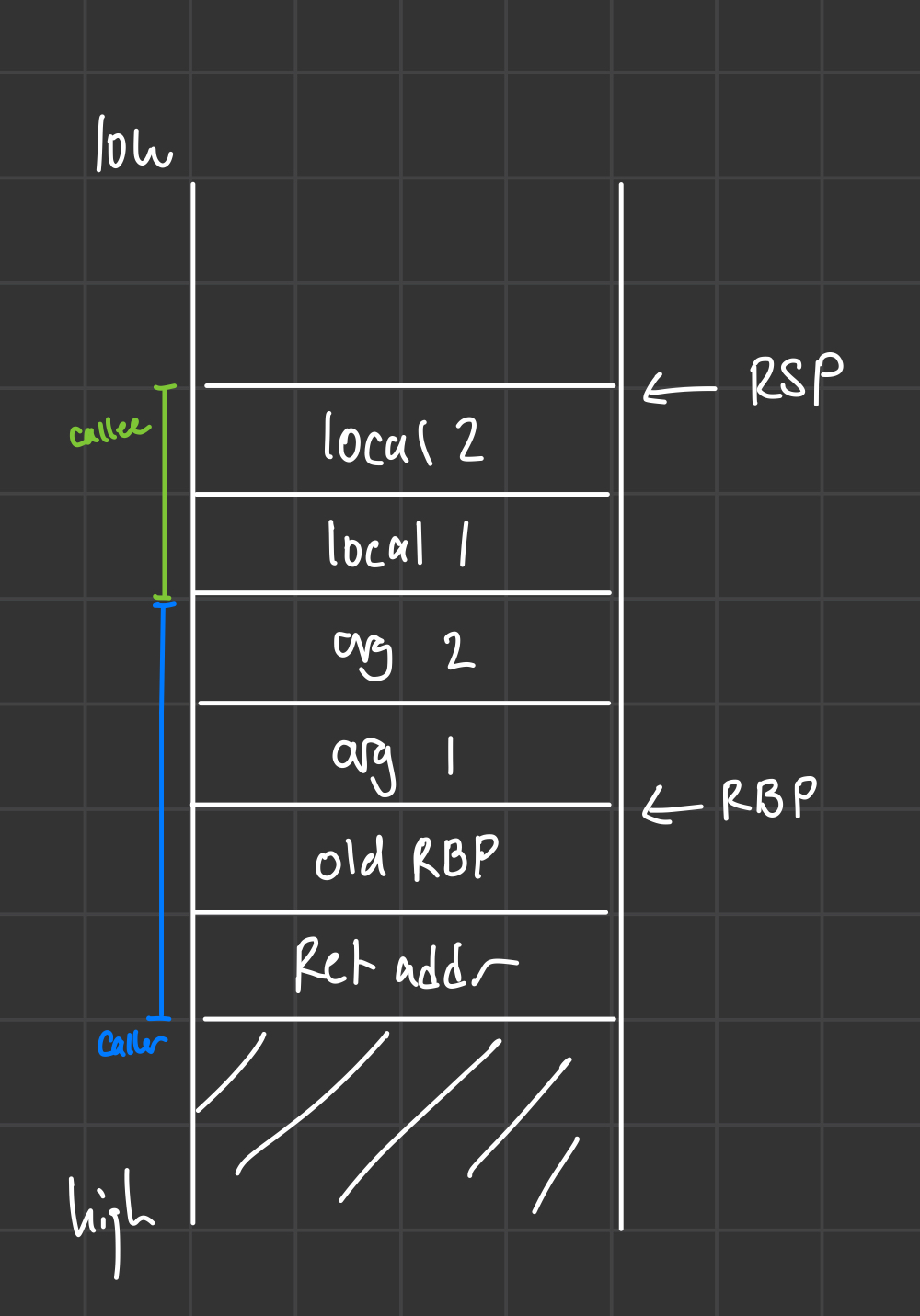
By doing so, restoring RSP using RBP will not only knock off all of the locals, but the arguments as well! We also will not have to shift the entire stack frame up when we make increasing arity tail calls, since we will just reserve more space for our arguments. Recall that our local arguments already were knocked off of the stack when we made tail calls before.

We now examine how the compilation of function calls and function declarations will change based upon this calling convention.

First, note that now the body of a function can find its first argument at $[RSP-8]$ and later arguments at $[RSP-8*i]$. The first local variable can be found at $[RSP - 8(M + 1)]$, where $M$ is the arity of the function being compiled currently; later local variables can be found at $[RSP - 8(M + i)]$.

To call a function, we can no longer use the call instruction, since that pushes on a return address and then jumps to some label. If we do so, we would be unable to put the arguments onto the stack! Therefore, we will have to push on the return address, then the old RBP value (storing the current RSP value as a new RBP), then each of the arguments (in order, this time) before jumping to a function. At this point in time, our stack looks like the following:

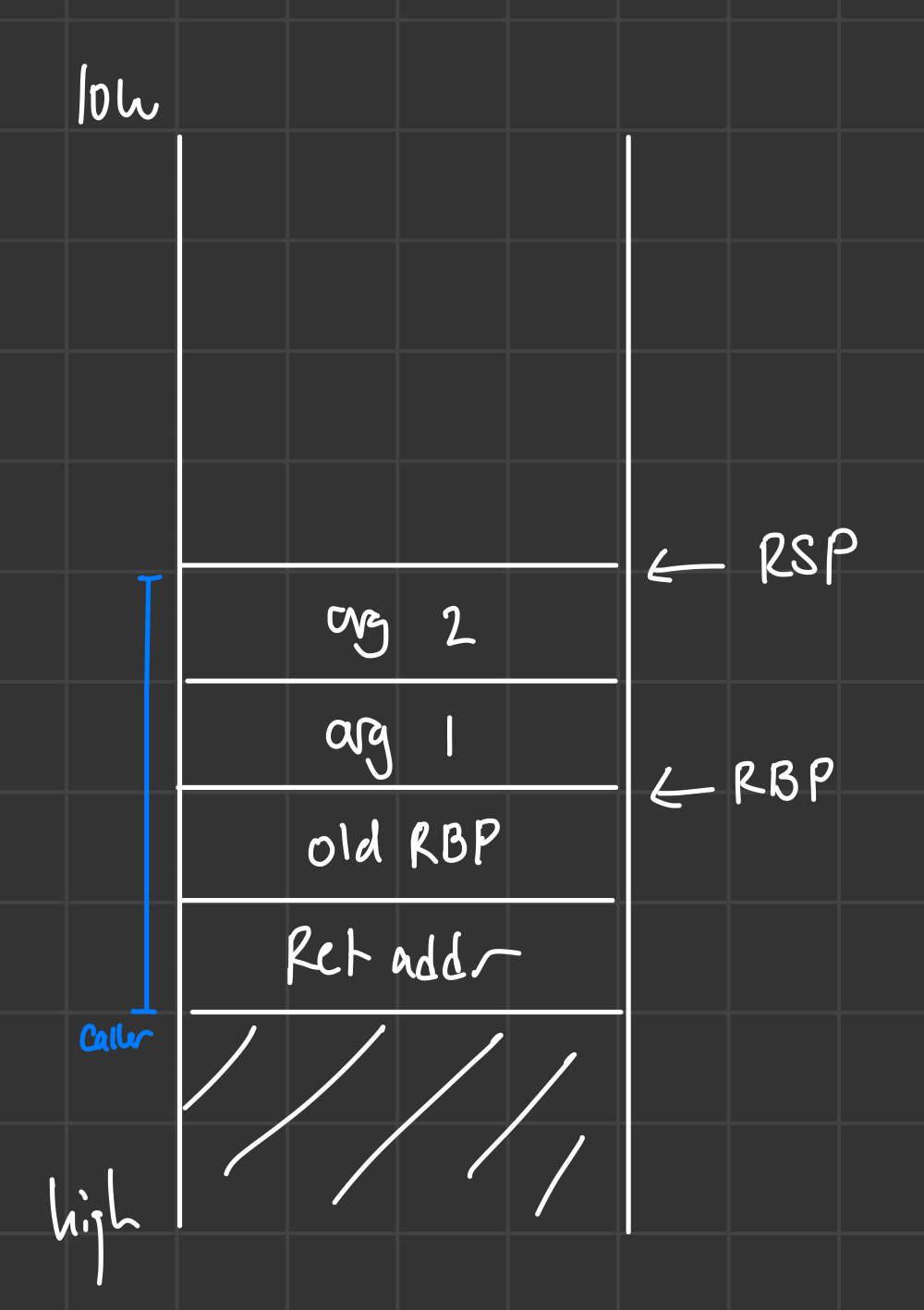
Now, the first thing that the called function should do is increment RSP by the necessary amount to reserve space for local variables, then perform the body of the function. When it is time to return, the called function can reset RSP down to RBP, pop the old RBP into place, and return to the address now on the top of the stack.

Implementation Pitfalls

A simple problem implied above comes as a ramification of being unable to use the call instruction. Notable, we now need to push a return instruction onto the stack, then continue to push arguments. The function should return to the caller after the arguments have been pushed, so we cannot just look at the instruction pointer. Instead, we can define a new label foo_returns_here to know the proper return address without having to do extra address math. We can push this label (which is just an address) onto the stack, and returning with ret will jump to that label.

Before, when we were loading arguments into other argument slots, we had to be careful not to load a new argument into a spot that would be used to load a later new argument. This issue is still present, and we need to be more cautious now that we can be loading arguments into slots currently occupied by local variables. Various techniques to tackle this issue are discussed in Lecture 9; the easiest of which is to push such arguments onto the stack and pop them into place.

Like before, we will have to be careful to keep RSP at a multiple of 16 whenever may need to call an external function (since those calls abide by the standard calling convention). We need the invariant that the return address will be 16-byte aligned, since the function we came from (represented by the shaded bottom of the stack in the image above) needed to be able to have called a C function; we must maintain this invariant when we increment RSP at the start of our function (since this function itself may call into C).

To do so, at the start of our function, we may have to push on an extra padding word. Specifically, we now need to look at not just the parity of the number of local variables (returned by deepest_stack in our working implementation), but the parity of the sum of the number of locals and the number of arguments (that is, the arity of the function we are currently compiling). Be careful of off-by-one bugs with alignment, and note that we do still push RBP on top of the return address.

Finally, since the first thing that a function body does is decrement RSP by its number of locals, we will still have to reset RSP below all of our locals, like above. Instead of being able to jump to RBP, we now have to use arities. Specifically, we should reset RSP to $[RBP - 8*(\texttt{foobar_arity})]$ before jumping to a function body foobar being called in tail position. Be sure to thoughtfully consider edge cases here!

Conclusion

The content of this note stems primarily from a discussion with Ben Lerner about the implementation of the Diamondback compiler:

The handwritten version of these notes can be accessed here.